Systematic & Unsystematic Risk And CAPM

If the CAPM correctly describes market behavior, the measure of a security's risk is its market-related or systematic risk. The CAPM provides insight into the market's pricing of securities and the determination of expected returns. Therefore, it also has a clear application in investment management. The model relates to a firm's cost of equity capital and the cost of equity for the market as a whole. The tool will arm you with a simple equation to assist you in optimizing your investment decision and the creation of your portfolio.

SYSTEMATIC & UNSYSTEMATIC RISK
Some of the companies in your portfolio may experience unanticipated adverse conditions, like an unannounced strike. This immediate adverse condition may be offset by unexpected good fortune of other firms in your portfolio. However, stock prices and returns tend to move in tandem, and not all variability can be eliminated through diversification.

It is preferable to divide a security's total risk into a portion that is peculiar to a specific firm and can be diversified away (called unsystematic risk) and that portion that is market related and nondiversifiable (called systematic risk):

Total risk =
Unsystematic risk (diversifiable risk, firm-specific) + Systematic risk (nondiversifiable risk, market-related)

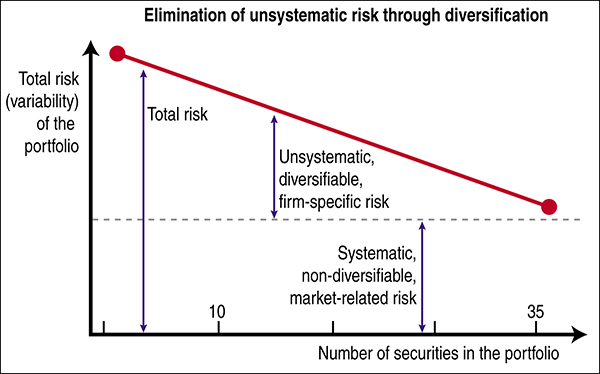
As the number of securities is added to a portfolio, the total risk is reduced. Our research indicates that unsystematic risk is minimized in portfolios of 35 (+/-5) securities drawn from industries that are not closely related. In general, holding 20 to 25 securities is a good rule of thumb, as most people cannot hold 30 to 40.

FIGURE 1: ELIMINATION OF UNSYSTEMATIC RISK THROUGH DIVERSIFICATION. As securities are added to a portfolio, the total risk is reduced. The remaining systematic risk is market related.

Accordingly, there is a close relationship between movement in the returns of any diversified portfolio and in the returns of market indexes. Some examples of systematic risk are boycotts, massive tax action, restrictive money policies, and skyrocketing interest rates. Some examples of unsystematic risk are the death of Steve Jobs, a wildcat strike of the United Auto Workers, Nokia suddenly enters the Microsoft market, and oil is discovered in your backyard.

RISK, RETURN, AND MARKET EQUILIBRIUM
You must be compensated for taking on risk with your hard-earned money. Risky securities are priced by the market to yield a higher than expected return than low-risk securities. The risk premium is necessary to induce investment in the security. The market is dominated by risk-averse investors. You do not want to lose your money. There must be a positive relationship between risk and expected return to achieve equilibrium. The expected return on a riskless security like a Treasury bill is risk-free.

The expected return = Risk-free return + Risk premium
R_S = R_F + R_P

In other words, the expected return will vary with the risk premium based upon the flat risk-free return. The curve can be linear or exponential, depending upon the risk premium investment.

CAPITAL ASSET PRICING MODEL
The CAPM is an idealized view of how the market prices securities and determines expected returns. It provides a measure of your risk premium and a method of estimating the market's risk-expected return curve.

The idea is that variations in returns from one security will likely be canceled by complementary variations in the returns of other securities in your portfolio. You are rewarded with a higher expected return for holding market-related risks. The result of the CAPM is that a security's return is related to the portion of risk that cannot be eliminated by portfolio combination.

CAPM provides a convenient measure of systematic risk. This measure is known as beta (β) and gauges the tendency of a security's return to move in parallel with the overall market's return. A good way to think of β is as a measure of a security's volatility relative to the market's volatility. If the stock has a beta of 1.0, it tends to rise and fall the same percentage as the market (for example, Standard & Poor's 500).

Accordingly, β = 1.0 indicates an average level of systematic risk. If beta is greater than 1.0, the stock will change more than the market changes and will have a high level of systematic risk, since there is greater sensitivity to market changes. A beta of less than 1.0 has a low level of systematic risk and is less sensitive to market swings. The results determine the risk-expected return tradeoff under the CAPM.

We know that R_S = R_F + Risk premium. Then the CAPM describes market behavior by

R_S = R_F + β (R_M − R_F)

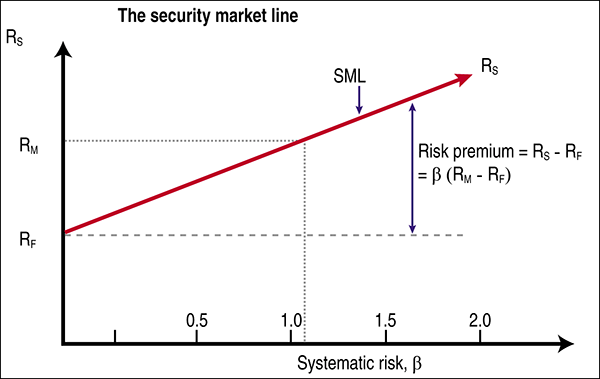
This equation states that the expected return on a security is equal to the risk-free rate (R_F) plus a risk premium. The risk premium is β times the return on the market (R_M) minus the risk-free rate. We can also restate the equation

R_S − R_F = β (R_M − R_F)

which is equal to the risk premium for security S. The risk premium on a stock or portfolio varies directly with the level of systematic risk, beta. The risk or expected return tradeoff with CAPM is called the security market line (SML). The SML is pictured in Figure 2.

FIGURE 2: SECURITY MARKET LINE. The risk premium on a stock or portfolio varies directly with the level of systematic risk, beta. The security market line (SML) shows you the risk or expected return tradeoff with CAPM.

This risk is unsystematic, because it is unique to this company. Since this stock's return is not closely related to the return on the market as a whole, it will contribute little to the variability of your diversified portfolio. Its unsystematic risk can be diversified away by holding a large portfolio. However, the costs of launching the vehicle and the price of fuel are related to the level of economic activity, and this stock does contain some market-related risk.

Most of the total risk is unsystematic related to the successful launching of the craft, even though the stock appears risky. In terms of total risk, it has a low level of systematic risk and the β might be 0.7. The market will price this stock to yield a relatively low expected return. If you hold a large portfolio, it is a low-risk security.

Consider a company that manufactures operating systems software. It is large and stable and its total variability in return is less than that of the spacecraft company. However, its sales, earnings, and stock returns are closely related to the changes in overall economic activity. The return on its stock is sensitive to changes in the return on the market as a whole. Its risk cannot be eliminated by diversification.

When this stock is combined with other securities in your portfolio, changes in its return reinforce swings in the returns of the other securities. It has a high level of systematic risk and a β of over 1, perhaps 1.6. Because of its high level of non-diversifiable risk, the market considers this stock risky. It is priced to yield a high-expected return. In general, most companies with high total risk have high beta, and companies with low total risk have low beta.

EXPECTED RETURN
The CAPM correctly describes market behavior as the relevant measure of a security's risk as its market-related or systematic risk as measured by β. If a stock's return has a strong positive relationship with the return on the market, a high beta, it will be priced to yield a high-expected return. Unsystematic risk can be eliminated through diversification and it does not increase a security's expected return. The market cares only about systematic risk.

Let us summarize the determination of expected return with the CAPM:

• Risk is defined as variability in return.
• You can reduce risk by holding a diversified portfolio. I ran an experiment over the last five months using students. The students were asked to select five securities from five different industries in two different portfolios. In one portfolio, the students were to select securities that would yield an average beta of greater than 1.2, and in the other portfolio, they were asked to select securities that would yield and average beta of less than 1.0.
  
  In the portfolio with a beta range of 0.8 to 1.6, the result over the period was a 38% loss in investment value. In the other portfolio with a beta range of 0.6 to 1.3, the result was a 17% loss in investment value. Other variables were kept constant.
  
  Although the students were amateur investors, their security selection followed generally accepted investment principles. Even with only five securities, the lower beta resulted in a minimized risk. Obviously, performance improvements in this study can be made with enhanced due diligence skills in security selection.


• Security risk can be divided into systematic and unsystematic risk.
  • Risk that can be eliminated by diversification is unsystematic risk. It is risk that is unique to the company and not related to other firms.
  • The remaining risk in a diversified portfolio is systematic risk and it is associated with the movement of other securities and the market as a whole.
• You hold diversified portfolios to minimize risk.
• Holding a diversified portfolio allows you to be exposed only to systematic risk. You are rewarded by a higher expected return only for holding systematic, market-related risk. There is no reward related with unsystematic risk, because it can be eliminated through diversification. Accordingly, relevant risk is systematic, market-related risk and is measured by β.
• The risk or expected return tradeoff with the CAPM is SML.
• Securities are priced by R_s= R_F + Risk premium or R_s = R_F = β(R_M − R_F)
• The SML will then give us an estimate of the expected return on any security, R_S

SUGGESTED READING

• Roll, Richard [1977]. "A Critique Of The Asset Pricing Theory's Tests," Journal of Financial Economics 4: 129-176.
• Sharpe, William F., et al. [1964]. "Capital Asset Prices: A Theory Of Market Equilibrium Under Conditions Of Risk," Journal of Finance 19 (3): 425-442.
• Subach, Daniel J. [2012]. "Diversification And Risk Reduction," Working-Money.com, April 2.

SIDEBAR: CONSIDERATIONS WITH CAPM
The capital asset pricing model (CAPM) assumes asset returns are normally distributed random variables. It is frequently observed that returns in equity and other markets are not normally distributed. As a result, large swings can occur in the market more frequently than the normal distribution assumption. The variance of returns is an adequate measurement of risk -- that is, returns are normally distributed or distributed in any two-parameter way. Risk in financial investments is not variance in itself. It is the probability of losing and is asymmetric in nature.

Potential shareholders' expectations are biased, causing market prices to provide inefficient information. This possibility is studied in the field of behavioral finance, which uses psychological assumptions to provide alternatives to the CAPM such as the overconfidence-based asset pricing model. It has been found that although an investor is more than 90% confident in security selection and performance based upon belief, the actual performance is substantially less.

The CAPM does not adequately explain the variation in certain stock returns. Empirical studies show that some low beta stocks may offer higher returns than the model would predict. In addition, the CAPM might not be empirically testable. This argument was presented by Richard Roll's 1977 paper.

The model focuses over a short-term horizon. If you have a longer-term outlook you might select long-term inflation-linked bonds instead of short-term rates, as this would be more risk-free. However, this action is individual investor imposed.

You must rebalance your portfolios over time, as the CAPM assumes that active and potential shareholders will consider all assets and optimize one portfolio. Individual shareholders tend to have multiple portfolios and a goal for each. It is usual to have multiple portfolios -- for example, an IRA, 401k, capital return, fixed income, and so on. You would just have a CAPM for each of your portfolios and plan review and rebalancing in the course of the normal investment process. The model was introduced by a 1964 article by William F. Sharpe and others.

The CAPM assumes that the risk-return profile of a portfolio can be optimized. An optimal portfolio displays the lowest possible level of risk for its level of return. Since each additional asset introduced into a portfolio further diversifies the portfolio, the optimal portfolio must make up every asset, with each asset value-weighted to achieve an optimized risk-return portfolio.