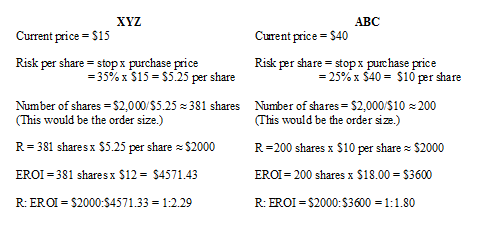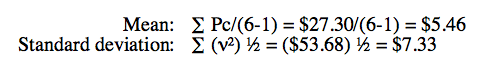HOT TOPICS LIST
- Strategies
- Stocks
- Buy
- Investing
- Brokers
- Psychology
- Interviews
- Accumulate
- Sell
- Hold
- Spotlight
- Websites
- Candlestick Corner
- Gold & Metals
- Options Trading
LIST OF TOPICS
MONEY MANAGEMENT
Position Size And Profitability
07/31/13 08:58:34 AM PSTby Bruce Tintelnot
Practicing good money management and analyzing your risks will make a difference in your trading results.
| Investing your hard-earned income in the capital markets is a big decision. Online brokerages make it easier than ever to do it on your own in minutes or even seconds by clicking your mouse a few times. Many investors and traders adopt a trading style of hitting for the bleachers, so to speak, which commits large amounts of cash to one or a few orders with hopes of large returns in a short amount of time. Even traders who are well educated in the fundamental and technical aspects of the markets are not immune to this tendency. In the forex market, many an investment account has turned into a large donation to a national or global economy in a brief timespan. But a situation like this could be avoided with good money management and a careful weighing of the risks when determining how large an order should be. HOW MUCH TO INVEST DETERMINING POSITION SIZE Say you decide to place an entry order for a stock that is $20 per share and place your stop at 25%, or $15. The amount that you have at risk is $5 per share ($20 minus $15). The number of shares that you would purchase for this order is your trading limit of $1,000 divided by the amount of your stop at $5 per share, which would equal 200 shares. The total amount that is invested is $4,000 (200 shares x $20), and you are only risking $1,000 (200 shares x $5) should the trade go against you. |
| RISK/REWARD RATIO How much you risk on an order in relation to its profitability should be decided beforehand and will depend largely on your comfort level or tolerance for risk. Unfortunately, some traders use their gut instinct for deciding their risk tolerance level. A better way would be to find a quantitative approach such as the risk/reward ratio. Most professional investors use this latter approach. They calculate a ratio that compares the amount of money willing to be risked on an investment to the expected return on that investment (EROI). If the ratio is considered favorable, then the investment is worth entering. Here's how the risk/reward ratio is calculated: Risk/reward ratio = R: EROI A 1:4 ratio shows that you stand to gain four times the amount you have risked investing, if the transaction moves in your favor. Optimal ratios can differ with different situations and strategies. Say an investor is considering purchasing stock in company XYZ that currently has a market price of $15 per share. He is expecting the price of this stock to rise by $12 per share to $27 in the near future. He is also considering a stock purchase in company ABC that is currently $40 per share and he expects it to rise by $18 per share in about the same amount of time as XYZ. He has a $100,000 trading account and is willing to risk 2%, or $2,000, in one of these stocks. The stop for XYZ will be at 35% ($9.75) and for ABC it will be at 25% ($30). The risk/reward ratio for each of these companies is displayed in Figure 1.
FIGURE 1: COMPARING RISK/REWARD RATIOS. Here, company XYZ has a risk/reward ratio of 1:2.29 and company ABC has a risk/reward ratio of 1:1.8. In this case, the investor uses a risk/reward ratio of 1:2 or higher for investment consideration. Company XYZ qualifies for his consideration with a ratio of 1:2.29, whereas ABC falls short with a ratio of only 1:1.8. Notice that the XYZ stop is a higher percentage than that of ABC. WHAT IS RISK? RISE OF BETA The benchmark, usually an index or another security, is considered to have a value of 1.0 and securities are given values that are usually above or below 1.0 indicating their volatility in relation to it. If a stock is given a beta of 0.75, it will most likely move only 75% up or down in relation to the movements of the benchmark. Conversely, a stock with a beta of 1.75 will move 175% in relation to each move of the market. If the market moved 1% for the day then the stock with a beta of 0.75 would only have moved 0.75%, whereas the stock with the beta of 1.75 will have moved 1.75%. Benchmark indexes can be chosen from any index that is relative to the investment you are considering. Some market indexes used as benchmarks for the beta are the NYSE Composite, S&P 500 for stocks, the NASDAQ composite for technical stocks, or JP Morgan Government Bond Index for bonds. It's always good to find out what index is being used. Over time, the beta of a stock can change as its volatility changes. A disadvantage of the beta is that the information to create it is historical, which makes it a bad predictor of the future, and since it changes with a stock's movements, it can be unreliable at times as it might suddenly flip around. These drawbacks make the beta more useful for the short-term investor than those using longer time frames. Small-cap companies have a greater degree of volatility than large blue chips, and this is reflected in their betas. The beta of a stock can usually be found with online stock quotes or published investor information services. |
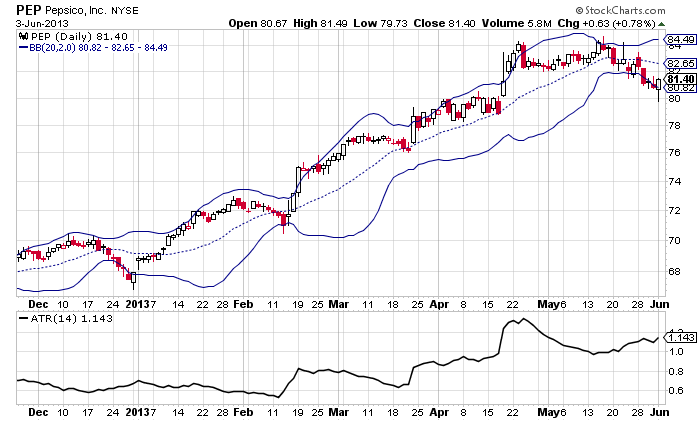
| STANDARD DEVIATION The standard deviation is used in two ways to express a security's risk. It can be used to measure the deviations of prices from the mean to express the market risk of a security, or it can be used to measure how the dispersion of actual returns deviate from expected returns for securities or any other investment. The standard deviation from the latter method is considered to contain market risk and unsystematic risk. When comparing two or more investments, you would use the standard deviation to measure market risk. Bollinger Bands provide a graphic representation of historical standard deviations from a 20-period moving average [MA(20)] of a stock or other capital market investment (Figure 2). They are found in most charting software or websites. The default setting is ±2.0 standard deviations from the MA(20) but that can always be changed. Bollinger Bands make it very easy to see how prices deviate from a mean, which in turn is helpful when it comes to creating trading strategies around volatility.
FIGURE 2: USING BOLLINGER BANDS TO DETERMINE VOLATILITY. Here you see the Bollinger Bands applied on the daily chart of Pepsico Inc. (PEP). Notice how prices react when they deviate from their mean. The standard deviation (SD) of a security's prices is a common measure for determining its volatility. Calculating the SD begins with computing the arithmetic mean of historical prices for a specific time period. Then each point or time period on the mean is subtracted from the corresponding closing prices that deviate from it to arrive at the variance. Each of these values are squared and then added together. The square root of this sum is the standard deviation. |
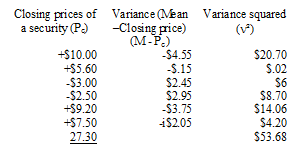
| Example (see Figure 3):
FIGURE 3: CALCULATING STANDARD DEVIATION. You can determine the risk of an investment by comparing standard deviation. The security with the higher standard deviation would be the riskier investment. The risk of two investments can be determined by comparing their standard deviations. The security with the higher standard deviation would be considered the riskier of the two. The previous example shows a security with a standard deviation of $7.33. If compared to a second company with a standard deviation of $5.95, the first company would be considered the riskier investment than the second one. These numbers can be turned into decimals if the values of Pc are entered as percentages. A drawback to using the standard deviation is in its underlying theory. It assumes that all of the returns on individual investments for a randomly distributed sample of transactions fit into the bell-shaped normal distribution curve. In reality, they might not fit perfectly. There could be occasional extraordinary gains that would be placed at either end of the curve (the tails) protruding above the graph and this would skew the results. This is something to keep in mind for any calculation or method that uses the standard deviation. THE SHARPE RATIO S = (R - Rf) / s The variables are easy to understand. The actual rate of return (R) and the standard deviation (s) are based on the historical data. The risk-free rate of return (Rf) is a benchmark that is used to express the opportunity to invest in another investment that has a low-enough risk to be considered risk-free or nearly risk-free. Benchmarks can be industry standards or market indexes, such as the S&P 500 or one of the Dow Jones averages. The rates of government Treasury bonds are often used as a risk-free rate for a benchmark because of the unlikelihood of the government defaulting, but their returns are low and they do change with economic conditions at each auction. When the Rf is subtracted from the actual rate of return, the difference is considered to be the actual market risk of that investment. In the example in Figure 4, there are two companies that an investor is considering for stock investing. One is a lower-priced, more volatile stock, and the other is higher-priced and more stable. The rate of return (R) for both companies is the same. Another security is available that is considered to be risk-free (Rf) with a return of 7.52%. The standard deviation is 0.6842 for ABC and 0.3333 for XYZ. After plugging all of the variables into the Sharpe ratio calculation, the two results show that although both companies had the same rates of return, ABC is the riskier investment of the two with a ratio of 0.7362 compared to 1.51 for XYZ. This is because ABC is more volatile, as seen in its higher standard deviation.
FIGURE 4: USING THE SHARPE RATIO. Would you buy a lower-priced, more volatile stock or a higher-priced and more stable one? The Sharpe ratio may help you make your decision. |
| WHICH ONE? It's always best to approach investing with tools to help you determine your position size and gauge the risk to your own comfort level and trading style. There is more than one way to do this. The risk/reward ratio lends itself well to this, making it is easy to calculate risk with respect to your position size. Volatility is what makes trading in capital markets for profits possible, and economic tools -- such as beta, standard deviation, and the Sharpe ratio -- create quantitative measures that are used by many investors and analysts for arriving at investment decisions. FURTHER READING
|
Bruce Tintelnot is a private trader and freelance writer.
PRINT THIS ARTICLE

|

Request Information From Our Sponsors
- StockCharts.com, Inc.
- Candle Patterns
- Candlestick Charting Explained
- Intermarket Technical Analysis
- John Murphy on Chart Analysis
- John Murphy's Chart Pattern Recognition
- John Murphy's Market Message
- MurphyExplainsMarketAnalysis-Intermarket Analysis
- MurphyExplainsMarketAnalysis-Visual Analysis
- StockCharts.com
- Technical Analysis of the Financial Markets
- The Visual Investor
- VectorVest, Inc.
- Executive Premier Workshop
- One-Day Options Course
- OptionsPro
- Retirement Income Workshop
- Sure-Fire Trading Systems (VectorVest, Inc.)
- Trading as a Business Workshop
- VectorVest 7 EOD
- VectorVest 7 RealTime/IntraDay
- VectorVest AutoTester
- VectorVest Educational Services
- VectorVest OnLine
- VectorVest Options Analyzer
- VectorVest ProGraphics v6.0
- VectorVest ProTrader 7
- VectorVest RealTime Derby Tool
- VectorVest Simulator
- VectorVest Variator
- VectorVest Watchdog